スポンサードリンク
|
|
前回の「高校数学の先取りは、理解できるかどうかに尽きる。」の続きです。
少し書き方が弱い所があったことと、歓談部屋でも「夏休み増刊号希望」の声、「今度はお姉ちゃん視点で」の声もありましたので、高校数学で脱落した私が語るのは非常に辛いのですが、「数学は暗記科目」について記載したいと思います。
数学は暗記科目である。
よくコメント欄でも、数学は考える力が必要とか暗記科目とか意見が飛び交っています。
ここでは、算数キングの親父さんのコメントを引用しつつ、数学(算数)の考える力と暗記について明確にしていきます。
引用理由ですが、単に私の説明より分かりやすいので(汗)。
算数キングの親父さん、いつもありがとうございます!
それが出来ていると、基礎問題は一通り解けます。
しかし、その次のステップは暗記です。
本番の試験は中学受験・高校受験では約45~60分で約8題程度の大問を解く事になり
1問に掛けられる時間は約5~7分です。
それでは、知らない問題は解けないのです。
これは大学受験でも同じで、1問の作業時間が延びるので試験時間が長いだけです。
大学受験の問題なら1問15~20分です。
当然、考える時間もありませんね、知らない問題は解けません。(ごく稀に天才がいますが)
小中なら、家勉でしっかりやった問題を覚えておいて、試験会場で瞬時に記憶から呼び出し
本番で5分で解くのです。
この記憶のポケットの量が少ないと、駿台の模試なんかだと点が取れないと思います。
塾の方針は、出来ない問題と格闘することによって記憶を定着させる方法で
これは、塾の好きな方法です。
理由は、指導者側が進捗スピードを管理しやすいからで大勢を指導するには向いております。
本来、個々の能力・進捗スピードは異なるのでベストを言うなら個別指導もしくは親の指導です。
しかし、現実は適性な教材を探すのにも一苦労するので、子供のレベルに合った塾に放り込む方が楽です。
まぁ、基礎が出来ているので後は覚えるだけです。
まぁ、何かアドバイスをするなら「出来なかった問題の正解答は3回書け!」って事くらいですね。
実際はやらしませんが、それが心構えと重要ポイントです。
要は「暗記科目」です。
先に言っておきます。
算数(数学)は、ちゃんと「理解している」っというのは当たり前の事です。
サラッと書かれていますが、これが凡人にはなかなか難しいことなんですよ。
正直、ここを突破したら、あとは実践あるのみじゃないですかね。
我が家の高校受験生。
良友や悪友達から、塾の数学の問題が送られてくるそうです。
読んで、この解き方かなって思いつき、その通りにゴリゴリ解いていったら解けたってパターン。
塾でやってないのに解けてしまう。初見の問題なのか?
ただ単に、解法の理解の差、記憶のポケットの量の差なんだと思います。
(ここの部分、不快になられた方がいましたらすみません…。)
解法を理解して暗記する。
これをひたすら繰り返すことで、模試では高得点が取れるようになってくるはずです。
そうそう、塾の夏期講習はえげつないですね。
通常の夏期講習にオプションがくっついてきて、〇〇集中特訓とか、親子の不安を解消させてくれるようなキャッチフレーズ。勿論、課金です。
高校受験もお金がかかります。
塾を全否定するつもりはありません。うちも、某T塾に行ってますから。
ただ、本当に必要なものとそうでないもの。必ず吟味したほうがいいでしょう。
数学(算数)の理解について考える。
理解ってどこまでを理解といえるのか?
まずは算数。
高学年は何度も言っている割合の分野です。
今回は、中学年について。
もう2年前かしら。末っ子がハイレベ100小学3年算数にある問題が解けないと訴えてきました。
その問題はこれ。

※以前も答え間違ってますよって指摘してきた方がいましたが、うちはいちいち消しゴムで消すのが面倒なので、解き直しは裏紙を挟んでいます。
末っ子が書いてあるのは間違った答えです。
さて、困ったのは公式バリバリの親。
・ケーキをx円、ジュースをy円と置くんだよ。
・x+y=430円
・4y-x=20円
これが小3小4の子にはとても難しいようです。
結局、当時小5か小6だった娘を登場させたところ、

あっという間に解いてしまいました。
私は上手く説明できませんので、メモ書きで許してください。
この話、どこかで書きたいと思ってたんです。
こうして、お披露目できて良かったです。
多分、今は方程式でバリバリ解いた方が手っ取り早いと思うはずです。
ハイレべで何度も泣かされた子ですが、理解できるまでコツコツ頑張ってきた成果が手に取るように分かります。

続いて高校数学。
私に講義してくれたメモです。
解説は諸事情によりしません。雰囲気だけお伝えします(汗)。
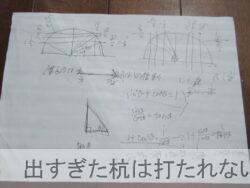
上記の算数と数学を例に出して分かるかと思いますが、理解する上でアチコチでコメント欄で話題になっている
「数量感覚」というものがとても大事になってきます。
身についていないと、算数キングの親父さんが「理解するのは当たり前」ってところまでたどり着けないんですよ。
歓談部屋から引っ張り出すのは大変なので(埋もれるお部屋ですのですみません!)、この辺のコメント欄を参考になさってください。
ちょっと!!誰とはいいませんが、書きこみされた方々!タイトルと全く違うじゃないですか!!
まあ、このサイトの良い所でもあります。
非常に勉強になりますので、是非ご覧になってください。
塾が大好きなキャッチフレーズ「考える力」とは。
T大卒夫に聞いてみました。
「数学って暗記科目なの?」
答えはYES.
算数キングの親父さんと全く同じことを言ってました。
入試の時に初見の問題ばっかりじゃ、時間内にとけないじゃんって。
もう一歩踏み込んで、
「でも、塾とか考える力を鍛えろって言うけど、どう思う?」
T大卒夫の答えは、
「暗記より考える力って言った方が聞こえがいいじゃん」
でした。
総論
算数・数学はどんな子でも時間をかける教科になっていくことは間違いないです。
もう、小学校低学年から算数・数学は始まっていると思っていいでしょう。
 Copyright secured by Digiprove © 2021
Copyright secured by Digiprove © 2021スポンサードリンク








管理人さん、こんばんは。
お姉ちゃん目線の数学を書いてくださり、
ありがとうございます。
私は嬉しくて、うちの長女と一緒に、
この記事を拝読しました。
うちの長女は、
管理人さんの長女さんのメモを見て
「この子、
私が方程式を使う前に、
算数の問題を解いていた考え方と、
同じ考え方で、問題を解いてる♥️」と、
嬉しそうに笑顔で言いました。
長女曰く
「ジュース5本から20円安いのが430円。
だから、
ジュース5本 買うと450円。
ジュース1本の値段は90円。
ジュース4本で360円。
360円から20円ひくと340円。
したがって、
ケーキの値段は340円。
と、いう考え方をしている」。
そして、長女は、
管理人さんの次男さんが書いた
線分図を見て、
「私、線分図を書く時は、いつも、
○と◻️の 2種類の記号を使って考えると
決めてたな~」と、
懐かしそうに言いました。
その後、長女は、満面の笑みで、
私を相手に、
小学算数トーク炸裂。
すごく楽しそうに
小学算数を話す長女を見て、
私は嬉しく思いました。
久しぶりに、長女と
小学算数トークで盛り上がり、
私も楽しかったです。
長女は、
管理人さんの長女さんと
会った事は無いけど、
自分と同じ考え方で
小学算数を解いている
同期生女子がいたという事を知り、
喜んでいました。
管理人さん、
お忙しい中、この記事を書いてくださり、
感謝しています♥️
連立方程式を知った長女は、
二度と小学算数には戻らず、
今後は、便利な
方程式しか使わないでしょう。
話は変わりますが、
数学キングさんレベルの人は、
「理解→暗記」で、
記憶のポケット量が多くなりますが、
我が子のように普通の学力の人は、
「計算力と記憶ポケット量」が
車の両輪です。
計算力が無いと、
暗記の効率が非常に悪くなります。
計算力が無いと、
解法全体の流れが掴めないから、
どんな条件の時に、
どんな解法を使うのか、
集中して考える事が出来ません。
長女は、中学生になってから、
計算力の大切さを痛感して、
「計算力を強化しない伸びない」と
言って、本人なりに、
色々 考え、努力しています。
長女は中学1年なので、
「本人に任せてみる事が必要な年齢」
です。
親は、
「子供の可能性を信じて待つ。
必要な時は、背中を、そっと押してあげる。
親が、ゆったりとした気持ちで、
どっしり構えいると、
子供も、伸び伸びと挑戦できる」
のかなぁ。と、思います。
亀田ゴロー、
第一子が中学1年なので、
このサイトで、母として、
中1娘との接し方を勉強させてください。
宜しくお願いします。
ゴローさん コメントありがとうございます。
ゴローさんの頼みでしたので、書く選択肢しかありませんでした。
この方程式を使う方法とそうでない方法。
どこかで書きたかったので、ちょうど良かったです。
こちらこそ、ありがとうございます。
中学受験でも、方程式を教えるかどうか?問題になるようです。
数学キングの親父さんは、教えてるんじゃないかなあ。
ゴローさんが書かれている通り、方程式を知っちゃうと、もう算数では解かない(解けない)問題の典型例かと思います。
お姉ちゃん、中学受験の算数やってない認識でしたので、どこまで力があるのか?ちょっと気になってたんですが、なかなかやりますね!
少なくとも、中学数学で躓くことはないでしょう。
塾も要らない(教えてもらう必要がない)と思います!
計算力は大事です。
遅いと高校数学は模試でも最後まで解けないことが致命傷になりますので。
大学受験の模試でも、とにかく時間が足りないとずっと言ってます。
本人が分かっているのですから、2年後はもっと速くなってるはず!
こちらこそ、また宜しくお願いします。
管理人さん、
ありがたいお言葉を頂き、嬉しいです。
中学受験で、方程式を教えるかどうか?
中学受験しなかった長女の
意見を聞いてみました。
長女曰く、
「長方形の面積を求める式や、
長方形の周りの長さを解く式は、
方程式の考え方の基礎となる。
したがって、
小学生に、
方程式を教える前に、
長方形や図形を勉強を強化する。
その後で、
方程式を教えた方が効率がいい。
それに、
長方形の面積を求める式は、
小学生が、
Xをイメージするのに
役に立つと思う。
長方形の面積=たて × よこ
長方形の面積 = Xとすると、
たて = 6センチ、
よこ = 3センチ。
長方形の図を書き、
その図に、
縦と横の長さも書く。
X = 6×3
= 18
長方形の図と、式を見たら、
小学生は、
Xをイメージしやすい。」
5ヶ月前まで、
小学生だった女子の意見です。
中学受験しない小学生でも、
中学生になれば、
数学の授業で、方程式を習います。
長女が言うには
「小学生の間に、
図形を強化しておくと、
中学数学は、理解しやすい」
そうです。
公立中学生の意見です。
参考になれば、幸いです。
話は変わりますが、
管理人さん、
計算の大切さを、
長男さんの貴重な体験談で教えてくださり、
ありがとうございました。
」
こんにちは。
本スレになかなかコメントを残さない建築好きです。
T大卒夫さまと我が家の主人同じこと言ってましたよ。
息子に、わからない問題でも間違っていいから一度は解いてみるように言います。
そこで、息子は、自分なりに考え問題を解くようにしています。そして、何回か間違ったり時間がかかったりしてるものには、少しだけヒントをだします。我が家の場合は、問題文の文章に大事なとこをやここの意味をしっかり考えればわかるよっと言うとこに線を引っ張るだけです。
あとは、自力で息子に考えるように仕向けています。
なぜ、このような方法になったかというと、子供のわかったがあてにならないからですね。
もともと、主人と話あった結果、上記の方法でわかれば、問題を理解する。これを積み重ねると、自然と文章で重要な場所なども読んだ時にわかるようになるからヒントの出し方は、上記の方法でやるっと言う話になりました。
建築好き様、こんばんは。
建築好き様の
お子様にヒントを出すコメントを
興味深く拝読しました。
建築好き様のヒントの出し方は、
私の長女が2年の時の担任の先生と
同じやり方です。
とても、いい方法ですね。
私は子供の年齢で、
ヒントの出し方を変えました。
私の場合、
子供が低学年の時のヒントの出し方は、
2種類ほどありました。
①子供に、規則性を見つけさせる。
小2で習う長さの問題。
「18センチは何ミリでせすか?」
この問題のヒントの出し方。
紙と鉛筆を用意し、
子供に「1センチは何ミリか、書いてね」
と、言う。
ポイントは「子供に書かせること」。
口頭は不可。親が書くのも不可。
子供が
「1センチ = 10ミリ 」と書いたら、
その下の行に、
1センチ = 10ミリ
18センチ =
と、子供に書かせる。
そうすると、子供は、
1センチの時、 10ミリだから、
18センチの時、180ミリ。
と、規則性を自分で見つけます。
そして、子供は自分で
1センチ = 10ミリ
18センチ =180ミリ
と、答えを出します。
同じく、小2の単元の「かさ」も同様。
子供が「わからない」と言ってきたら、
紙と鉛筆を用意し
子供に「1リットルは何デシリットルか、
書いてね」
と、言う。
このヒントの出し方だと、
子供は、自力で規則性を見つけ、
自分で答えを出します。
②線分図や図形を正確に書く。
ポイントは「適当は不可」。
長女には小学校6年間、
これは意識させました。
小2の単元「時間」の問題。
「午前5時から午後8時まで、
何時間ありますか?」
子供が「わからない」と、言ってきたら、
紙と鉛筆を用意し、
子供に線分図を書かせる。
ポイントは「子供に書かせること」。
口頭は不可。親が書くのも不可。
子供は、線分図を書いたら、
子供は勝手に自分で
線分図の左に「午前5時」と、書き、
線分図の右に「20時」と書きます。
ポイントは、時計の問題で、
子供が「わからない」と言ってきたら、
線分図で考えるやり方で統一する事。
私は、日常の時計の勉強も
同じ方法で考えるよう、子供に
声かけしています。
ここまできたら、親は子供に
「線分図の、どこを考えるの?」と、
声を掛けるだけで、
子供は「ここを求める」と、自分で
線分図に線を書き、
自力で答えを出します。
子供が低学年の時、
私は、このような感じで
ヒントを出しました。
しかし、子供が高学年になったら、
大人に頼らず、
自分だけで答えに辿りついて欲しいですよね。
私は子供が高学年の時、
子供の学力に合った
「参考書と問題集がセットになっている」
教材を買いました。
子供が「わからない」と言ってきたら、
まず、親は
「わからない時は、何を調べたらいい?」と、
子供に聞きます。
子供は、参考書を見て、
わからない問題を解こうとします。
参考書を見ても、どうしても解らない問題だけ
大人が教えます。
ポイントは
「高学年になったら、大人に頼らず
勉強する事が大切だから、何を使えば、
それができるか、自分で理解し、
実行すること。
それでも解らなかった場合だけ、
大人に聞くこと」と、子供に伝えること。
あとは、管理人さんが仰る通り、
日々の勉強で、
解決ポケットを増やすことが大切ですね。
解決ポケットがなかったら、
ヒント以前の話になりますね。
話は変わりますが、
私は子供の小学校のテストやプリントは、
「子供の小学生の時の思い出」として、
全部、保存しています。
娘の小1の時の担任の先生が、
そのようになさっていて、
担任の先生が仰るには
「子供が成人したら、
子供が小学生の時の
テストやプリントを見ると、
その当時の事を懐かしく思い出すから、
私の宝物です」。
よろしければ、建築好き様も、
お子様の学校のテストなど、
思い出として、保存しておくと、
将来、素敵な宝物になるかも♪
それでは、これからも、色々 勉強させてください。
なんの事かと思ったら。。。
あぁ~この記事ですね。
数学は暗記科目!
さすがご主人素晴らしいですね~
刮目する思いです。^^
ありがとうございました!
管理人様、こんにちは。
前回は青チャの件でお返事有難うございます。
数学の勉強の進め方を解説して頂いて、やっと理解できました。
公式バリバリの親、私のことでしょうか?理解しないで、公式を当てはめようとしてたから数学が苦手だったんだと納得です。
学校は、中学数学が終わったら高校数学に進む前に、演習を集中的にやると説明されたのを思い出しました。きっとこの演出=暗記なんですね。
高校数学の本は、買わないでいたら学校の図書館で色々借りて来てました。
こんにちは。さん ゴローさん 建築好きさん Zさん コメントありがとうございます。
遅くなりました。
こんにちは。さん、みてくださいましたか。
ほぼパクリ、おっと、間違えた。コメント欄のまとめです。
「公式丸暗記≠数学は暗記である」
これはZさんがかかれている通りですね。
私も中学数学までは通用しました。でも、高校数学で落ちぶれた原因はこれだと思ってます。
あ、Zさんより私の方が高校数学が苦手だと思います。
もうね、愚息は目を輝かせて私に講義してくれるのですが、難しすぎてついていけません(涙)。
私立中高一貫生の数学の授業の進み方を教えてくさりありがとうございます。
定着演習があったりと入試を意識したカリキュラムに気が引き締まります。
つい最近、「大学受験は先取りできているから、むしろ高校受験がハンデかも」なんて言ってきました。
いや、逆でしょ。中高一貫生との勝負だよって言ったら納得していましたが。
つい最近、なんで中学受験の算数は方程式教えないんだろうねって話になりました。
公式丸暗記の子を排除?のため?
機械的に当てはめる数学は伸び悩むから?と今は思うようになりました。
また続きます。
管理人様のコメント「なんで中受の算数は
方程式を教えないんだろうね」の件。
数日前の歓談部屋で「こんにちは様」が
(中受する》子供さんに方程式を教えたと
仰っていました。
中受組も、中受の算数の問題は、
「方程式で解ける問題は、方程式で解く」。
我が家は、親子とも中受未経験です。
管理人さんのお兄ちゃんは、
友達を通して、
中受した子から情報を聞いているから、
私達より中受組について詳しいと思います。
前回の管理人さまのコメントで、
つい最近、(管理人さまのお兄ちゃんと》
なんで中受の算数は方程式を教えないのか
と、話しました。
(中略》
また続きます。
と、書いてありました。
管理人さまの時間がある時でいいので、
「また続きます」のコメントを書いてくださると
助かります。
管理人さまは忙しいので、いつでもいいです。
遅くなっても大丈夫です。
宜しくお願いします。
横からすみません
何度も断っていますが、私は算数(数学)、英語は全く守備範囲外(不得意科目)なので
自分の言葉で亀田ゴローさんの疑問に答える事ができません
ただ、算数(数学)の本質を分かっている方(算数の神(中学入試問題に捨て問題無しの解答解説をしてしまうレベル、ラスボス)、算数の神に中学受験算数の基礎を教えてもらいました。他算数、数学を通して知った尊敬している方々)の共通して言われている事で中学受験界隈では有名な方のコラムを見つけたのでリンクを貼っていきます
算数の本質を理解している方々と共通する事を書かれているので、私の低レベルな受験算数の理解度の人が書くより信用度が高いと思います
『プレジデントオンライン 中学受験で足を引っ張る理系父の口癖』で検索してみてください。
一部抜粋
算数とは、数少ない道具を使って、それらをいろいろ組み合わせながら答えを探すものだ。そこでは「今わかっていることから、次は何がわかる?」「それがわかっているなら、何がわかる?」といった頭の使い方をする。順を追いながら答えを見つけていくため、道筋がはっきりしていないと答えを出すことができない。ビジネスでいうと、「今あるリソースで何ができるか」を考える創造的な発想だ。つまり、外へ考えを広げていく拡大思考だ。
一方、数学は、決まった形の方程式の中に数字を入れて、計算をする。「答えを出すためには、どういう式ができればいいのか?」「条件を当てはめられるか?」といった頭の使い方で、多くは公式に終結させる。テンプレートにそって作業を進めていく手法と捉えることができる。つまり、中心に向けて絞り込んでいくという集約思考だ。
このように、両者は考える方向が違うのだ。受験算数は結論を出すよりも、限られた道具(条件)を使って、工夫をしながら解くことに意味がある。使える道具が少ないからこそ、考え工夫する力が鍛えられる。その試行錯誤する姿勢こそが、難関校をはじめとする多くの学校が求める生徒像であり、その力があるかどうかを見極めるために入試が存在するのだ。
残りは、コラムを読んで頂ければと思います
コレは算数、数学が得意な方の書かれていた事ですが、私の解釈なので箇条書きでごめんなさい
もっと、理論的に書かれてあって分かりやすい文章ですが再現はできなかったです
算数(受験算数)の思考が、数学の思考に役立っている。
算数と数学は別モノではなく、連続性である
東大の入試問題を中学入試にも出題される事が多々ある
←東大の入試問題からもわかるように、『思考力』がしっかりできる生徒を求めている
中学入試も『思考力』がないと解けない出題が多いという事になる
中学受験算数の関連した界隈をウロウロしていると、東大入試問題から中学受験算数に使われている問題の解説記事を読む機会があり見ていて面白いです
難関校と言われる学校のレベルのすごさ(東大入試レベル)、それを少ない道具を使い解いていってしまう手腕ですからね(レベルの違いを見せつけられます)
小学生でもきちんと解けるような解き方をしているから神レベル(私の尊敬する方の解き方になります)
小学生の頃に算数に落ちこぼれ、中学、高校と数学に向き合わず(学生時代に勉強した事なく社会人になってから勉強をして、勉強法を知った人)
だから、子供と一緒にやり直し組なので、算数も数学も新鮮で楽しくって仕方がない私
多分、子供以上に私の方が楽しんでいると思う
子供の進路は、親が情報を与えていくけれど子供の人生、子供が決めていけば良いと考えているので受験算数は私の趣味(やり直し算数)です
そこに子供を巻き込ませて好き勝手やっている感じで、何処にどう転がっていくかは不明
大学は目標が確固たるモノがあるので、その分野のTOP校を目指していったらと情報は与えていっています(大学に入学するまでのキャリアパスは子供の選択肢に私はサポートしていくだけです)
脱線長くなってきたので
失礼いたします
出てきた理由は、小学生に方程式を教えない理由について説明ができない自分にモヤモヤしていたんです
私が、気づいた受験算数の本質をきちんと言葉にしてくれた記事を見つけられたので出てきた次第
算数は少ない道具を使って、如何に工夫していけるかを試行錯誤していく教科で他の教科の考え方の礎になっていると思うのです
福嶋式(論理国語)と算数の考え方に共通点があって、理科や社会でも応用できる事を記事にしていました
算数お父さん(仮称、算数の神とは別の方ですが、算数指導(塾の先生)プロにもお墨付き)がいて
私もその共通点を理解してからは、子供に教えるのに自信がついたのと
その共通点を意識して鬼の千本ノック(子供への質問と対話をしていっています)をしています
番外編1ですので
呼ばないで下さいね
番外編2は時期がきたら出てくるつもりでじっくり待ちの状態(スリープモード)
わかる方にはわかると思うのでメッセージを残していきます
だから呼ぶな
呼ばれても出る予定は無し
お願いです
呼ばないでね
呼ばないで下さいね
管理人さんのサイト乗っ取るつもりは無いから
ひっそりと読み専で居たいんです
本音
だから、帰らせてください‼︎ネ
wwww wwww wwww
草かげ様、丁寧に回答してくださり、
ありがとうございました。
感謝いたします。
ひとことで言うと
「中受の算数は、学習指導要領の範囲を
越えてはならないから、原則、方程式を
教えない」と、いう事ですね。
私の子供は全員、中受しません。
私は、我が子に
「算数(数学》をやると、頭がよくなり、
抽象的な思考力が伸びる」から、
算数(数学》の勉強を通して、
「物事を俯瞰し、抽象化し、
分割し、整理できる」人に
育って欲しいです。
歓談部屋の「数学女王」
悩める母さんの名言で
「わからない」の根底は「わけられない」。
悩める母さんの数学談義で
「東大数学でも、基本的には
教科書を理解しておけば、
わかるようになっている。
教科書の定理を、
どのように使うかというのは、
演習をすると、わかりやすい」と、
教わりました。
我が家では、
子供との家庭学習で、
子供が解けない抽象的な問題は、
子供が分かる所まで落とし込むように
しています。
これは、管理人さまから教わった事ですが、
「わからない所で、
ずっと立ち止まっても、
ずっとわからないまま。
先に進んだら、見えてくるものがある。
とりあえず、割りきって、
先に進む」
悩める母さんの数学談義でも、
数学女王は同じことを言ってました。
今回、草かげ様の数学談義を拝聴し、
勉強になりました。
草かげ様、親切に教えてくださり、
ありがとうございます。
小学生に方程式を教えない理由についてをコメントしていきましたが
私個人の考えを追記させて下さいね
結論を先に書いてしまうと
小学生に方程式を教える事には私は全く反対する気持ちはないです
仮定の話しです
私が算数(受験算数を含)、数学が得意で教えられる(得意と教えられるかは別だと思っているのです)場合、指導要領、中学受験算数なんて気にせず
子供の理解具合を見ながらですが、小学生だからという理由で中学、高校数学を教えないという事はしないです
中学受験で私学に方程式で式を書いた場合の対応を聞いた記事があり、解いたとしても採点をします(0点や減点とかしない)という実体もあるようなので
子供が算数(受験算数)を理解していて、数学的解き方をしても混乱せず中学受験で算数の解き方、数学の解き方の使い分けができるので有れば中学受験が終わるまで数学をやらないという理由にはならないです
中学受験勉強をしつつ、数学も教えていってしまいます
中学受験をするか、しないかが決まっていない場合でも、子供の理解を見てある一定のレベルになったら数学を教えていってしまいます
実際は私は算数も数学も自分が出来ない、やり直し組なのでそんな事は無理なのでやらないだけです
教えられる大人が近くに居て、子供もしっかり理解できるのであれば、小学生に方程式を教える(数学)のは悪くはないと考えています
←条件が大人も子供も揃っている場合の話です
みんながみんな同じ理解ではないからです
子供が数学が好き、得意で、理解力があるようであれば私は自分では教えられないので個別指導の先生(家庭教師)を使ってドンドン先に進めていっています
←例えば(極端かも知れませんが)小学生の内に中学数学を終わってしまう位に得意とか
1を聞いて10理解できる能力があって算数(受験算数含む)をガンガン理解できるとか
の能力があって、数学の事ばかりを考えているような位にのめり込んでいくタイプというのでしょうか
いわゆる、算数小僧みたいな子供とか
凡人の子供はそんな能力も才能も無いので、コツコツとやっていっているだけです
亀田ゴローさんのお子さんの算数から数学への過程は良いなと考えています
長々と失礼いたしました
草かげ様、大切な事を教えてくださり、
ありがとうございます。
草かげ様が貼ってくださったリンクの言葉、
「算数、大好き。面白い」。
これがないと、小学生は勉強しません。
高学年以降は、この気持ちがないと、
自走しません。
小学生や中学生にとって、
算数や数学を勉強するのに、
最も大切な事ですよね。
草かげ様の優しい人柄が伝わる言葉を
書いてくださり、ありがとうございました。
車のワイパー透かして見てた
都会にうず巻くイルミネーション
くちびる噛みしめタクシーの中で
あなたの住所をポツリと告げた
September rain rain
九月の雨は冷たくて
September rain rain
想い出にさえ沁みている
どーも、愛子ちゃん!
9月になると
九月の雨
を繰り返して聴いてしまうのは愛子ちゃんと同様です。
石川ひとみバージョンもナカナカ良いですよ。
本日、うちのおねーちゃんは☆を受けに行きましたよ。
午後からの受験、天気も良く試験会場も知っているとノンビリしていたらJRアプリから
遅延発生
の通知があり、慌てましたよ。
本命の大学受験は全滅もあり得るので生きる道を探っていますが、ほぼ無勉なので厳しいですね。
実際、スラスラ解けたわけでもないようです。
では、
アディオォォォス!
F91さん コメントありがとうございます。
どーもです。愛子です。9月の雨は冷たいです。
はあ?ちょっと待って!!
とりあえず、最近、このサイトはアレ防止のため、☆をいれることにしております。
皆さん、ごめんなさい。
埋もれる場ではないので、肝心なところはとりあえず☆にしておきます。
大学以外の道も考えなきゃっておっしゃってましたが、驚きです。
いや、無勉の☆と大学受験では、どう考えてもおねーちゃんは大学受験の方が可能性は十分に高いのですが、生きる道という言葉をみて、何というか。
そう簡単にどうこう言えないなあって。
ここまで考えている親ってなかなかいないんじゃないかなと。
本当に行動に移されているとは。突き刺さりました。
写真だけ撮ってまだ全く書いていないのですが、今度は某T塾の模試を少し掲載したいと思ってます。
F91さんにも見ていただきたく。
おねーちゃんのようにビビるような点は取れませんが、それでも少し上がってきました。
F91さんがおっしゃっていた、「高校生に混じって勉強することの意義」が理解しました。
本当にありがとうございます。
こちらの夏休みですが、巷で言われているような10h勉強は程遠かったです。
6h7hぐらいが限界。
高校数学をやった日は、高校受験勉強は3hぐらい。
それでも、本人なりに頑張ったと思います。
追伸
石川ひとみバージョン。歌が上手いですよね。ついでに、想い出のセレナーデも聞いてしまいました。
ゴローさん 草カゲさん コメントありがとうございます。
>「また続きます」のコメントを書いてくださると助かります。
しまった!続きますって書いて忘れてましたわ。
ごめんなさい。
こんなことがありましたら、遠慮なくおっしゃってください。
「中学受験で足を引っ張る「理系父」の口癖 」を読みました。
本文に書いてあることがそのまま再現されてましたね。
うちは、方程式を教えても理解できなかったというオチがついていますが(汗)。
うちは中3の7月で数Ⅲが終わりました。
公式が山盛りなので、公式を暗記しないといけませんが、丸暗記だと高得点は取れないと何度も言ってます。
まあ、某T塾の有名講師が言ってるのだとは思いますが。
数弱の私が語るのは非常に苦しいのですが、、、。
まず、四則計算は大事です。
速く正確に計算出来ないと、話になりません。ハッキリ言って論外です。
絶対にどこかで落ちぶれていきます。
計算マシーンはその他大勢の仲間入りです。
うちは、ハイレべや最レべ、トップクラス問題集を3人それぞれやり、自由自在3・4年、高学年と進んでいます。
高校受験組ですが、やってることは中学受験組と変わりません。
違うのは、解法を暗記するまでやり込んでないだけ。
無制限の時間内で解いて、解けた!で終わってます。
中学受験組はこれじゃ駄目でしょう。試験には時間制限があるのですから。
これは合不合を受けた時に家族で出した結論です。だから中学受験組は大変なんだと。
中学受験の算数を吹っ飛ばして、数学に入ってもいいのですが、上記に書いてあるように、公式(解法)を理解するという部分で、どうしても思考力(理解する力)が必要になってきます。
この部分が非常に大きいかと。
中学数学ですら実感しているようです。
個人的には、中学受験の算数は是非やるべきかと思ってます。
導入時期は、高学年からならスムーズかといったらそうでもなく。
その他大勢の子達は、5年の抽象的な割合で躓くんです。いや、もっと前の4年生か。
この頃から学校の抽象的な問題が解けず親子で焦って塾通いです。
ちなみに、ハイレべ1年の算術特訓が解けない高学年は多いと思います。
後回しにすればするだけ、その他大勢の仲間入りで、ここからの挽回はそんなに簡単ではありません。
逆に、ここでその他大勢の子達が挽回できたら、誰もが行きたい大学に行けるはずです。
本文で書いた算数キングの親父さんの話ですが、どうやら方程式教えてるようですが、方程式を使わない方法もみっちりやってるかと。
都合よく、親父さんのコメントを解釈したら火傷しますね。
ゴローさんのおうちは、しっかりと算数を学んでいるので、中高一貫生のようにスムーズに数学はいけるかと。
算数を学んでなくて、数学で高得点を取りたい場合は、理解に時間がかかるかもしれませんが、主人もよくいう、理解するまでやり抜くこと。
あとは演習問題をガンガンやって、高校受験組も中高一貫生と同じ土俵で大学受験を頑張りたいですね。
管理人さま、お忙しい中、
方程式の続編を書いてくださり、
ありがとうございました。
感謝いたします。
管理人さまの仰る通り、
計算力は、とても大切だと思います。
計算力の有無で、
算数《数学》の勉強に費やす時間が
大幅に異なるから、
小学生の場合、
計算力が無いと、
「算数の勉強時間が長い」という理由で、
算数が嫌いになっちゃいますよね。
私も、大学受験を考えたら、
小学算数の計算力と、中学数学の計算力は
必須だと思います。
話は変わりますが、
本編に書いてある、
数学は「理解→暗記」と、いうのは、
「問題を、パッと見て解ける」
状態を指すのでしょうね。
問題をパッと見て、解けないのは
「理解→暗記」していない。
問題をパッと見て、解けるようになるには、
管理人さまが仰る通り、
演習をガンガンやり、
↓
「理解→暗記」する。
そして、「理解→暗記」した後、
↓
本編に書いてある「記憶ポケット」を
増やす。
↓
記憶ポケットが増えたら、
↓
問題を見たら、瞬時に、
「どんな条件の時に
どんな解法を使うのか」
記憶ポケットから出でくる。
管理人さまの長男さんが仰る
「丸暗記だと高得点は取れない」と
いうのは、
暗記の段階で止まっちゃうと、
問題を見ても
瞬時に「記憶ポケット」から
正しい解法が出てこない
と、いう意味かな?
《間違っていたら、申し訳ありません》
管理人さんが仰る
「中受の算数は、是非やるべき」と
いう御意見、
「理解→暗記」で、ストップしないで、
「どんな条件の時に、
どんな解法を使うのか」
記憶ポケットを増やす練習に、
中受の算数は、
とても効果があると思います。
管理人さま、お姉ちゃん目線の数学、
とても勉強になりました。
お忙しい中、貴重な内容を書いてくださり、
ありがとうございます。
管理人さまの長男さんは、
数学がデスクイで、素晴らしいです(^-^)/